Urinal protocol vulnerability

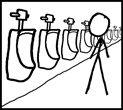
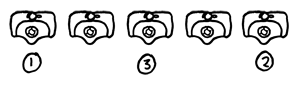
When a guy goes into the bathroom, which urinal does he pick?  Most guys are familiar with the International Choice of Urinal Protocol.  It’s discussed at length elsewhere, but the basic premise is that the first guy picks an end urinal, and every subsequent guy chooses the urinal which puts him furthest from anyone else peeing.  At least one buffer urinal is required between any two guys or Awkwardness ensues.
Let’s take a look at the efficiency of this protocol at slotting everyone into acceptable urinals.  For some numbers of urinals, this protocol leads to efficient placement.  If there are five urinals, they fill up like this:

The first two guys take the end and the third guy takes the middle one.  At this point, the urinals are jammed — no further guys can pee without Awkwardness.  But it’s pretty efficient; over 50% of the urinals are used.
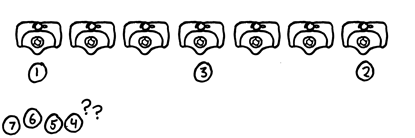
On the other hand, if there are seven urinals, they don’t fill up so efficiently:

There should be room for four guys to pee without Awkwardness, but because the third guy followed the protocol and chose the middle urinal, there are no options left for the fourth guy (he presumably pees in a stall or the sink).
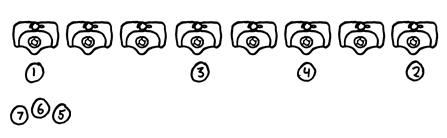
For eight urinals, the protocol works better:

So a row of eight urinals has a better packing efficiency than a row of seven, and a row of five is better than either.
This leads us to a question: what is the general formula for the number of guys who will fill in N urinals if they all come in one at a time and follow the urinal protocol? One could write a simple recursive program to solve it, placing one guy at a time, but there’s also a closed-form expression.  If f(n) is the number of guys who can use n urinals, f(n) for n>2 is given by:

The protocol is vulnerable to producing inefficient results for some urinal counts.  Some numbers of urinals encourage efficient packing, and others encourage sparse packing.  If you graph the packing efficiency (f(n)/n), you get this:

This means that some large numbers of urinals will pack efficiently (50%) and some inefficiently (33%).  The ‘best’ number of urinals, corresponding to the peaks of the graph, are of the form:

The worst, on the other hand, are given by:

So, if you want people to pack efficiently into your urinals, there should be 3, 5, 9, 17, or 33 of them, and if you want to take advantage of the protocol to maximize awkwardness, there should be 4, 7, 13, or 25 of them.
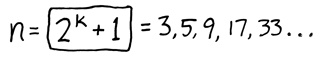
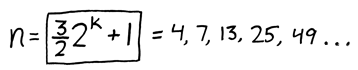
These calculations suggest a few other hacks.  Guys: if you enter a bathroom with an awkward number of vacant urinals in a row, rather than taking one of the end ones, you can take one a third of the way down the line.  This will break the awkward row into two optimal rows, turning a worst-case scenario into a best-case one. On the other hand, say you want to create awkwardness.  If the bathroom has an unawkward number of urinals, you can pick one a third of the way in, transforming an optimal row into two awkward rows.
And, of course, if you want to make things really awkward, I suggest printing out this article and trying to explain it to the guy peeing next to you.
Discussion question: This is obviously a male-specific issue.  Can you think of any female-specific experiences that could benefit from some mathematical analysis, experiences which — being a dude — I might be unfamiliar with?  Alignments of periods with sequences of holidays? The patterns to those playground clapping rhymes? Whatever it is that goes on at slumber parties? Post your suggestions in the comments!
Edit: The protocol may not be international, but I’m calling it that anyway for acronym reasons.